1页PPT、3分钟演讲，89岁阿蒂亚爵爷的黎曼猜想证明是闹剧还是天才？-大数据文摘的财新博客-财新网

文 | 蒋宝尚

德国柏林时间9月24日上午9点45分，菲尔兹奖与阿贝尔奖双料得主、英国皇家学会院士迈克尔·阿蒂亚爵士在德国海德堡举行的海德堡奖诺贝尔奖获得者论坛上，讲述了他对黎曼猜想的证明。

演讲视频截图

在论坛上，阿蒂亚爵士的演讲时间为45分钟，其中25分钟在回顾历史，而证明只有一页PPT。关于证明方法，他在演讲中表示，中心的证明方法是反证法。证明的关键点是引入了TODD函数。

这次证明，学界的质疑声比较高。因为无论是演讲中的证明介绍，还是贴出的5页预印本都没有能拿出令人信服的证明。

主要是两个方面，一个是TODD函数，这个函数是老爵士自己新建立的，在预印本中写到，因为过程太复杂，所以就不展开讲了。另一个是他提到的精细结构常数α，这个常数是物理学领域中的应用，且是一个浮动的数值。简单来说，他所用到的常数，在学界也没有得到完全的证明。另外，他关于精细结构常数的相关论文尚未通过同行审议。

但是也有学者表示阿蒂亚爵士的思路或为后续黎曼猜想证明提供了一种新思路。

文末给出了网传老爷子的证明预印本，注意这份预印本资料没出现在官方渠道上，也没有权威人士确认这份资料的真实性，真假还无法辨认。

黎曼猜想证明事件前后

今年的9月份，菲尔兹和阿贝尔奖得主迈克尔·阿蒂亚爵士宣称自己证明了黎曼猜想，并在9月24日海德堡获奖者论坛上宣讲。

消息一出举世震惊，因为黎曼猜想自1859年提出以来，到今天已有一百五十多年的历史了，这期间一直都没有解决。这一猜想也被列为世界7大数学难题之一。另外六个难题是NP完全问题、霍奇猜想、庞加莱猜想、杨-米尔斯存在性和质量缺口、纳卫尔-斯托可方程、BSD猜想。这七大难题都被悬赏一百万美元。

这个百万悬赏项目是2000年5月的时候，美国克雷数学研究所（Clay Mathematics Institute, CMI）设立的一个“千禧难题”的数学问题挑战。

当然，不是随随便便就能宣称“我证明了难题”，题解必须发表在国际知名刊物上，并且要通过2年的验证期和专家小组的审核。

现在只有庞加莱猜想被证明，证明者是俄罗斯数学家格里戈里·佩雷尔曼。

黎曼猜想所以被认为是当代数学中一个重要的问题，主要是因为很多深入和重要的数学和物理结果都能在它成立的大前提下被证明。大部分数学家也相信黎曼猜想是正确的。

对这一高大上的理论证明看起来和我们的生活没有什么关系。在这文摘菌想借用马云在阿里巴巴云栖大会演讲上的一句话：没有数学为基础，科学就没有基础。

无论是阿里巴巴设立达摩院青橙奖和全球数学竞赛，还是黎曼猜想被证明的消息震惊世界，其实都在说明一个问题，即业界和学界对数学越来越看重。

黎曼函数和素数的关系

让我们看一下黎曼猜想：

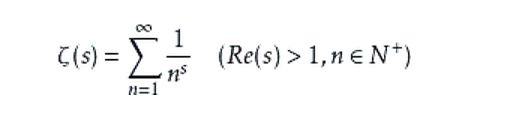
这个函数表达式中，s的实部大于1，如果实部小于1，那么这个级数是不收敛的。另外n取边所有的正整数。

这个猜想是：黎曼函数ζ(s)的全部非平凡零点，全部位于实部为1/2的一条直线上

这里的平凡零点是某个三角sin函数的周期零点；非平凡零点是Zeta函数自身的零点。

那么黎曼猜想和素数的分布又有什么关系呢？让我们来看它另一个变形公式：

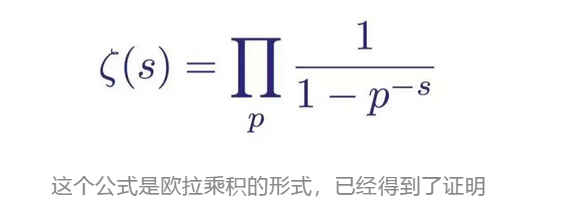
公式中的P为素数，又称为质数，是指大于1的自然数中，除了1和它本身以外不再有其他因数。例如3、7、11等数。

结合方程与根的关系，这就意味着，这个公式蕴涵着有关素数分布的重要信息。

没错，这就是黎曼函数的零点和素数分布联系到一起的根源。

所以，黎曼猜想最主要是解决素数分布的问题，数学界在之前一直认为自然界中素数的分布，肯定有着一种规律，但是这种规律只是目前还没有被发现而已。黎曼猜想等于是在说，素数最大的规律，就是没有什么突出的规律，素数的分布完全是完全随机。

大学修过概率论与数理统计的同学应该知道，在随机事件的大量重复出现中，往往呈现几乎必然的规律，这个规律就是大数定律。通俗地说，这个定理就是，在试验不变的条件下，重复试验多次，随机事件的频率近似于它的概率。大数定律将频率和概率联系了起来，偶然中包含着某种必然。

所以，黎曼猜想意味着，素数的分布必然也遵循着大数定律！！！

在这里也说明一下，随机和分布满足一定的规律并不矛盾。例如你投掷枚硬币，出现正面和反面的情况是完全随机的，但是出现在正面或者反面的概率趋于1/2。

证明难点

为什么黎曼猜想经过了159年，且无数科学家为之奋斗都没有证明？

这个猜想证明的难点在于主项是集合概念的命题是无法证明的，因为集合概念的每一个个体不是必然具有这个概念的基本属性。就决定了必须一个个去证明。

这就是说，必须对每一个零点都进行证明，在没有计算机之前，对于这种计算都是人工来算，计算机出现之后，人力得到解放，计算能力也大大提高，现在最新的成果是法国团队最新的成果是法国团队用改进的算法，将黎曼Zeta函数的零点计验证了前10万亿个，仍然没有发现反例。

虽然相比于最初哈代的学生1041个的计算记录，10万亿个零点的验证是巨大的飞跃，也更能够坚定人们对黎曼猜想的信任。但是，10万亿相对于无穷大，仍然没有绝对的说服力。

而采用分析思路证明的最佳的成果也只是证明了41.28%的非平凡零点分布在“临界线”上。

黎曼猜想不仅构建数学大厦

在一些顶级数学难题中，大家所熟悉的费马猜想（现在已经被证明了，所以是费马大定理了）和哥德巴赫猜想。

这是因为，费马大定理和哥德巴赫猜想的题目容易理解，即拥有中学数学的基本知识就能理解。费马大定理的数学表示是：n >2时，关于x, y, z的方程 x^n + y^n = z^n 没有正整数解。哥德巴赫猜想是：任一大于2的偶数都可写成两个素数之和。正是如此简单的数学表达，才能有如此深远的传播度。

费马大定理的证明，历经三百多年。期间为了证明这个法国律师和业余数学家提出的问题，无数的数学家为之努力，极大的推动了数学的发展。例如有人说数论中算术代数几何的这一数学分支的产生就是为了证明费马大定理。所以费马大定理当之无愧是数学界的“会生金蛋的母鸡”。

而在学界，学者公认的是黎曼猜想比费马大定理的数学地位更重要。因为一个半世纪以来，人们在假设黎曼猜想成立的情况下，以它作为基石，已经建立了一千多条定理，并且打造了无比辉煌的数论大厦。然而一旦黎曼猜想找到反例被证伪，这些精美的大楼就会如空中楼阁一样昙花一现，最终崩塌，给数论带来灾难性的结果。

还有一个是因为黎曼猜想研究的素数与密码的加密有着非常重要的关系。而加密无论是银行数据还是国家机密，还有号称最安全的区块链技术都会用到。

有些加密技术与大数分解有关。而大数分解加密采用的更多是素数分解。例如100这个数字，如果给你2*2*5*5这个公式，你很容易想到他的结果是100，但是如果直接给你100呢，他可以分解成的因子就会有很多，例如10*10、2*5*10。100这个数字可能很容易把结果穷举，但是如果这个数值是123587136412.......呢？所以黎曼猜想被证明对于素数加密领域也会非常大的震动。

另外，最出人意料的，是黎曼猜想的重要性不仅是在数学领域，而对于物理学也非常重要 1972年，人们发现与黎曼猜想的相关研究（孪生质数对在数轴上的分布规律）与多粒子系统在相互作用下，能级分布规律的函数有着显著关联。这种关联的原因直到今天也还是一个谜。但是在黎曼猜想与物理学的关系，无疑就进一步增加了黎曼猜想的重要性。

附录