编译：蒋宝尚、茶西

上图是万圣节的一周，在捣蛋和给糖之间，数据极客们在社交媒体上为这个可爱的网红词汇而窃窃私语。

你觉得这是个玩笑？让我告诉你，这不是笑料。这是吓人的，真正的万圣节精神！

如果我们无法假设我们的大部分数据(商业、社会、经济或科学根源) 至少近似“正态”(即它们是由一个高斯过程或多个这样的过程的总和产生的)，那么我们就完蛋了！

简单来说吧，以下非常重要的概念将无效~

• 六西格玛的概念

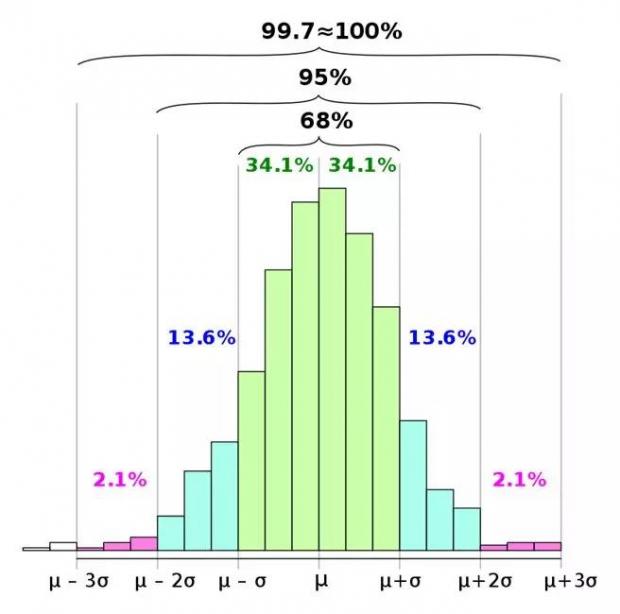
• 著名的68-95-99.7规则

• 统计分析中p=0.05(来自2西格玛区间)的“神圣”概念

够吓人了么？那我们再多说两句…

正态分布（高斯分布）是最广为人知的概率分布。在数据科学的圈里，数据科学家非常喜欢这个分布。

一方面是因为，符合这个分布的现象在自然界随处可见。在概率统计方面，中心极限定理撑起了一片天，而中心极限定理的最重要的一个假设是数据的分布符合中心极限定理。

最重要的一点是：简洁。

因为无论是正态分布的性质还是表达式都非常的简洁：

• 它的均值（mean）、中值（median）和众数（mode）都相同

• 只需要用两个参数就可以确定整个分布

这看起来都挺棒的啊，有什么问题吗？

问题是通常是，你可能会找到特定的数据集分布，这些分布可能不满足正态性，即正态分布的性质。但由于过度依赖于常态假设，大多数业务分析框架都是为处理正态分布数据集而量身定做的。

假设你被要求检测来自某个流程(工程或业务)的一批新数据是否有意义。所谓“有意义”是指新的数据是否属于它的“预期范围”，或者在它的“预期范围”之内。

我们自动如潜意识驱使般，测量样本数据集的均值和标准差，并继续检查新数据是否在一定的标准偏差范围内。

如果我们必须在95%的置信区间下工作，那么我们很高兴看到数据在2个标准差内。如果我们需要更严格的界限，我们检查3或4个标准差。我们计算Cpk，或者我们遵循六西格玛线的ppm(每百万零件数)的质量水平。

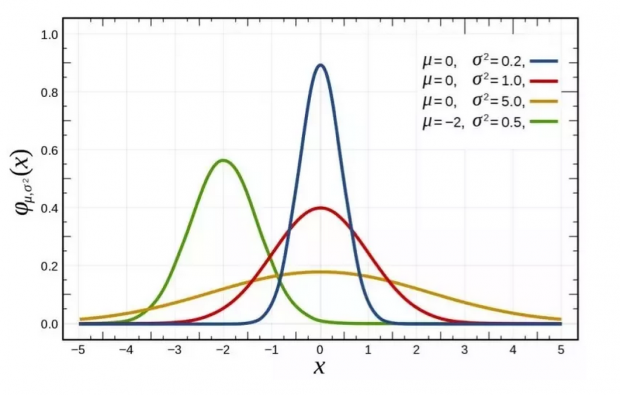
所有这些计算都是基于一个隐含的假设，即人口数据(而不是样本)服从高斯分布，即生成所有数据的基本过程(过去和现在)受下面左侧图的支配。但是，如果数据在遵循右侧图形会发生什么呢？

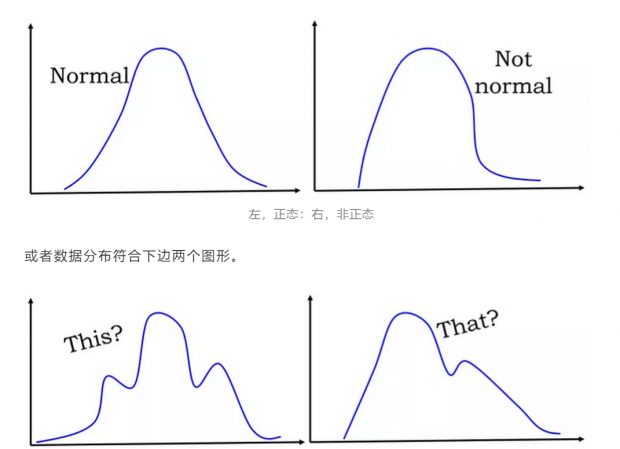
或者数据分布符合下边两个图形。

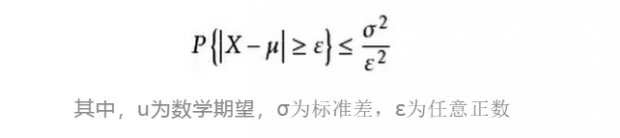
当数据非正态时，是否有更普遍的界限呢？

最终，即使数据是非正态的，我们仍然需要一种数学上完整的方法来限定我们的置信区间。这意味着，我们的计算可能会有一点变化，但我们还是应该能说出这样的话：

“与平均值一定距离处观察一个新的数据点的概率就是这样和这样的…”

显然，我们需要寻求一个比珍贵的68-95-99.7的高斯界限更普遍的界限(对应于与平均值的1/2/3标准差距离)。

 幸运的是，还真有一个这样的公式，叫做“切比雪夫不等式”。

切比雪夫不等式(也称为Bienaymé-Chebyshev不等式)可以确保，对于一类广泛的概率分布，不超过某特定分段的值会比均值的特定距离大。

大学生必修课《概率论与数理统计》里是这么说的：

切比雪夫不等式可以使人们在随机变量X的分布未知的情况下，对事件|x-u|<ε概率作出估计。

表达式是这样的：

它适用于几乎无限种类型的概率分布，并在比正态更宽松的假设下工作。

正如你现在可以猜到的，数据分析的基本机制不需要改变。你仍将收集数据样本，并且越大越好，计算 以前也会算的均值和标准差这两个量，然后应用新的界限，而不是68-95-99.7规则。

该表如下所示(这里k表示许多偏离平均值的标准差)：

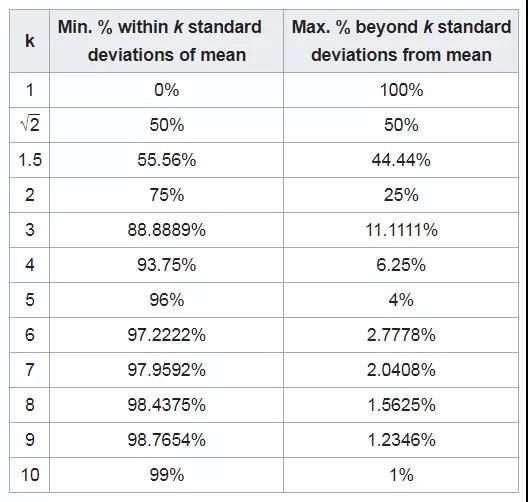
K均值标准差内的最小百分比/超出k均值标准差的百分比

痛点在哪呢？为什么人们不使用这种假设更弱的约束呢？

通过看表格或数学定义痛点很明显。切比雪夫规则在数据界的问题上比高斯规则弱得多。

首先，与正态分布的指数下降模式相比，它遵循1/k² 的图形。再例如，要以95%的置信度设定界限，需要包含最多4.5标准偏差的数据，而对于正态分布只需要2个标准差。

总体来说，在数据不是正态分布的时候还是挺有效的。

那么，我们还有别的选择么？

当然，还有切诺夫界以及Hoeffding不等式，它给出了独立随机变量和的指数锐尾分布。

当数据看起来非正态分布时也可以用来代替高斯分布，但只适用于有高置信度，且数据相互独立的情况。

不幸的是，在许多社会和商业案例中，数据有非常强的相关性。

在本文中，我们学习了一种特殊类型的统计界限，它可以应用于最广泛的数据分布，而不依赖于正态假设。当我们对数据的真正来源知之甚少，并且不能假定它遵循高斯分布时，这是有用的。因此，它是分析随意类型数据分布的重要工具。

相关报道：

https://towardsdatascience.com/what-if-your-data-is-not-normal-d7293f7b8f0